GMAT Geometry Problem Shortcuts
GMAT geometry problems tend to be one of the scariest of the Quantitative topic areas. Fortunately, all the geometry you need to remember could fit in the palm of your hand. Since you can’t actually put it in your palm on Test Day, here are some tricks for tackling GMAT geometry without notes.
Geometry problems with lines and angles
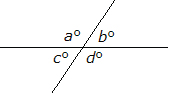
If you are given a figure such as this, with no angle measures provided, all you would know is that certain pairs of angles sum to 180° and the sum of all four angles is 360°.
There is no way to determine the measures of individual angles, so answer choices other than 180° or 360° will not be correct.
Finding the area of triangles
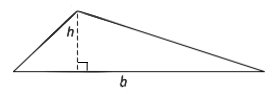
The formula for the area of a triangle is
A triangle’s base and height must be perpendicular (meeting at a 90-degree angle). Right triangles are the only type of triangle that have side lengths as base and height. For all other triangles, consider one side the base and then draw in a line for the height.
Equilateral triangles have equal side lengths and angle measures; because all triangles have an internal angle sum of 180°, each angle in an equilateral triangle is 60°.
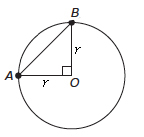
Isosceles triangles have two equal sides, and they also have two equal angles. Any time the GMAT presents a triangle with one vertex at the center of a circle, the triangle will be isosceles as each side will be the radius of the circle.
Quadrilateral figures
The formula for the area of a quadrilateral (four-sided figure) is (base)(height).
Base and height must also be perpendicular for polygons other than triangles. In a rectangle, all angles are 90°, but in a parallelogram (a figure with two pairs of parallel sides) that is not a rectangle, you must draw the height just like with a triangle.
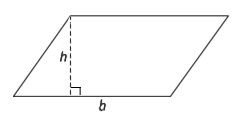
Rectangles and squares are types of parallelograms, ones where all the angles are equal.
Formulas for circles
The formula for the area of a circle is
and the formula for the circumference is 
.Some people have trouble keeping the two important equations straight when they encounter a circle geometry problem on the GMAT, so here is a mnemonic to help you remember:
You have to raise your voice an octave or so when you say “too” at the end, to remember that the 2 is an exponent. Give it a try
Circle component ratios
Circles found in the Quantitative Reasoning section are often drawn with a central angle marked; in the figure below, the central angle is X. Angle X measures n°. Points A and B along the circle’s circumference represent the arc. Imagine that this circle is a pizza and the shaded area represents one slice. The arc is the crust on one slice of the pizza. The slice itself, bordered by the arc and the central angle, is called a sector.
The measure of the central angle represents a fraction of the measure of the whole circle (360°), and the length of the associated arc represents the same fraction of the circumference (2πr). The area of the sector is also the same fraction of the area of the circle (πr²).
Looking at the circle above, let’s say n=60°. What fraction of the entire circle is that?
This central angle is ⅙ of the circle. Using the pizza analogy, if a pizza is cut into 60° slices, it is cut into 6 slices. The area of one slice is ⅙ of the area of the entire pizza. Its arc represents ⅙ of the circumference of the pizza, or ⅙ of the crust.
These three fractions can be written as follows:
Together, they form the circle ratio that you need to know for some of the GMAT’s geometry problems.
Now let’s go back to our circle above and take it further. Let’s say the diameter of the circle is 12. That means the radius is 6, the circumference is 12π, and the area of the circle is 36π. We can use these values to solve for the arc length by plugging the numbers into the ratio:
Solving for arc length by cross-multiplying and dividing, we find arc = 2π. We can then do the same thing to find the area of the sector:
Solving for the sector area by cross-multiplying and dividing, we find sector = 6π.
The formula for the volume of a rectangular solid, such as a cube, is
For a cylinder, it’s 
Instead of memorizing those formulas, all you really need to do is remember this one: for any solid on the GMAT, v=(area of base)(height). The base of a rectangular solid is a rectangle, and the area can be found using
Multiply that by the height and you have
For a cylinder, the base is a circle with area
. To find the volume, multiply that area times the height, or 
Using your critical thinking skills while reviewing content during your prep can be as important as using it while answering questions!
Every line on a coordinate system can be expressed in the form y = mx + b where m is the slope and b is the y-intercept (that is, the point where the line crosses the x axis).
Be sure you are comfortable with the relationships between parallel and perpendicular lines in the coordinate plane. Lines that are parallel have the same slope; they continue at the same slope to infinity and never cross. A line that is perpendicular to another line has a slope that is the negative reciprocal (change the sign and flip the fraction) of the other line’s slope.
For example, y = 23x + 4 will be parallel to all other lines that share a slope of 23. A line that is perpendicular to y = 23x + 4 would have a slope of -(1/23), which you find by changing the positive sign to a negative and taking the reciprocal of the fraction.
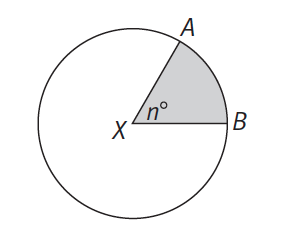
The measure of the central angle represents a fraction of the measure of the whole circle (360°), and the length of the associated arc represents the same fraction of the circumference (2πr). The area of the sector is also the same fraction of the area of the circle (πr²).
Looking at the circle above, let’s say n=60°. What fraction of the entire circle is that?
This central angle is ⅙ of the circle. Using the pizza analogy, if a pizza is cut into 60° slices, it is cut into 6 slices. The area of one slice is ⅙ of the area of the entire pizza. Its arc represents ⅙ of the circumference of the pizza, or ⅙ of the crust.
These three fractions can be written as follows:
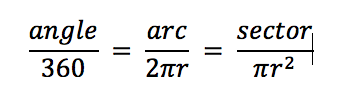
Together, they form the circle ratio that you need to know for some of the GMAT’s geometry problems.
Now let’s go back to our circle above and take it further. Let’s say the diameter of the circle is 12. That means the radius is 6, the circumference is 12π, and the area of the circle is 36π. We can use these values to solve for the arc length by plugging the numbers into the ratio:
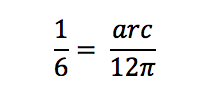
Solving for arc length by cross-multiplying and dividing, we find arc = 2π. We can then do the same thing to find the area of the sector:
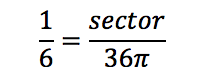
Solving for the sector area by cross-multiplying and dividing, we find sector = 6π.
Finding the volume of a solid
The formula for the volume of a rectangular solid, such as a cube, is
For a cylinder, it’s Instead of memorizing those formulas, all you really need to do is remember this one: for any solid on the GMAT, v=(area of base)(height). The base of a rectangular solid is a rectangle, and the area can be found using
Multiply that by the height and you have For a cylinder, the base is a circle with area
. To find the volume, multiply that area times the height, or Using your critical thinking skills while reviewing content during your prep can be as important as using it while answering questions!Coordinate geometry problems
Every line on a coordinate system can be expressed in the form y = mx + b where m is the slope and b is the y-intercept (that is, the point where the line crosses the x axis).
Be sure you are comfortable with the relationships between parallel and perpendicular lines in the coordinate plane. Lines that are parallel have the same slope; they continue at the same slope to infinity and never cross. A line that is perpendicular to another line has a slope that is the negative reciprocal (change the sign and flip the fraction) of the other line’s slope.
For example, y = 23x + 4 will be parallel to all other lines that share a slope of 23. A line that is perpendicular to y = 23x + 4 would have a slope of -(1/23), which you find by changing the positive sign to a negative and taking the reciprocal of the fraction.
Jennifer Mathews Land has taught for Kaplan since 2009. She prepares students to take the GMAT, GRE, ACT, and SAT and was named Kaplan’s Alabama-Mississippi Teacher of the Year in 2010. Prior to joining Kaplan, she worked as a grad assistant in a university archives, a copy editor for medical web sites, and a dancing dinosaur at children’s parties. Jennifer holds a PhD and a master’s in library and information studies (MLIS) from the University of Alabama, and an AB in English from Wellesley College. When she isn’t teaching, she enjoys watching Alabama football and herding cats.
