Finding Your Way Around GMAT Perimeter Questions
Perimeter questions on the GMAT are a subset of a subset–a small part of the geometry you will inevitably run into on the Quantitative side of the test. Perimeter is the distance around a geometric figure and on the GMAT is just that: the sum of the side lengths of a two-dimensional figure (three dimensional figures have surface area instead). They are in the category of “easy things made hard”: it is not challenging to add up the side lengths of a polygon, even an irregular one, so the GMAT will force you to infer the information you need to answer the question. Let’s look at some of the ways different figures’ information can be used to create perimeter questions.
Quadrilaterals
Quadrilateral means “four sided” in Latin, and it may not surprise you to learn they have four sides. Most of your GMAT quadrilaterals will be rectangles (which are parallelograms with four right angles), and many of those same rectangles will be squares (which have four equal side lengths). The formulas you need to know for quadrilaterals are:
Perimeter = a + b+ c + d, where a, b, c, and d are side lengths. If the quadrilateral is a rectangle, you can simplify the formula to 2l+2w, where l is the length and w is the width. If the rectangle is also a square, the perimeter is simply 4s, where s is a side length.
Area Area (rectangle) = l x w ; area (square) = s^2
Many quadrilaterals can also be broken down into triangles, where the formulas for those can also come in handy. I will be covering triangles (and those formulas) later on in this series. The important things you should note in problems with quadrilaterals:
1. Are there four right angles? If the problem says rectangle or square, you can assume there are four right angles because they are in the definitions of those two words. If not, look for the little square in the angle to show that an angle is a 90 degree angle.
2. Are the sides the same length? If so, a lot of the math is easier. Do not assume that all rectangles are squares, though!
3. Do you have actual numbers, or just variables and ratios? As with Quant in general, ratios and the numbers they represent can be very different. Make sure you have what you need to answer the question being asked!
Quadrilateral Practice Question
The perimeter of square ABCD is half of the perimeter of quadrilateral EFGH. What is the perimeter of quadrilateral EFGH?
1) a line segment drawn from the center of ABCD to the midpoint of BC is 2 inches long
2) a line segment drawn from the center of EFGH to the midpoint of FG is 4 inches long
Answer and Explanation
The answer is (A), that statement 1 is SUFFICIENT, but statement 2 is INSUFFICIENT.
As always with Data Sufficiency questions, we need to look at the statements individually first:
Statement 1: Because ABCD is a square, the distance from the center to any side’s midpoint is exactly half the distance of one side (and since it’s a square, all sides are the same). Since the line from center to BC’s midpoint is half a side length, BC itself is twice that distance.
2*line segment = length of BC = 4
4*BC = perimeter ABCD = 16
The perimeter of EFGH is twice that of ABCD, so perimeter of EFGH = 32. SUFFICIENT.
Statement 2: The statement tells us that the length of EG is 8 (twice the line segment parallel to it), but EFGH is a quadrilateral, which means that it has four sides that are not necessarily the same length. If EFGH is also a square, then knowing the distance from the center to the midpoint of a side is sufficient, but if it is not, then we lack any information about the length of the other two sides. INSUFFICIENT.
Circles
Circles are common on the GMAT because of one peculiar trait: if you get any one of the area, the perimeter, the diameter, or the radius, you can figure out the rest. The formulas you need for circles, as they relate to perimeter (which on circles is called circumference):
Area (circle) = πr²
Diameter (d) = 2r
Circumference: 2πr or πd
A circle has 360°, which means that if you are given or can compute two of: the length of an arc, the circumference of the circle, or the measure of the angle creating the arc, you can compute the third item. This, combined with the trait mentioned above, gives the GMAT test-makers tremendous flexibility in the creation of questions. They can give you little bits of information and expect you to derive the rest.
Circle Practice Question
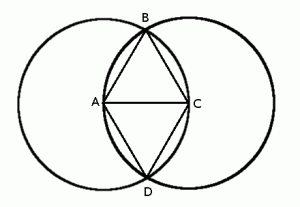
In the figure above, angles BAD and BCD each equal 120°, points A and C are the centers of their respective circles and are points on the opposite circles, and line segment AC = 3. What is the perimeter of the exterior of the figure, without any of the lines within?
(A) 16π
(B) 12π
(C) 8π
(D) 4π
(E) It cannot be determined from the information given.
Answer and Explanation
The answer is (C) 8π. How?
The perimeter of the figure will be the perimeters of the two circles, minus the portions of the circles that cross each other. If we can figure out the circumference of the circles and the lengths of the arcs, we will have our answer.
Perimeter of the circles: since A and C are each circle centers and points on the opposite circle, AC is the radius. The circumference of each circle is 2*π*3 = 6π.
Arc portions that overlap: since a circle is 360° and the angles creating the arcs are 120°, the angles and their arcs are 1/3 of the whole. 1/3 of 6π is 2π.
Full circle perimeter = 6π
Two full circles = 12π (answer choice B, a trap)
Arc length = 2π
Two arc lengths: 4π (answer choice D, a trap)
Two full circles minus two arc lengths = 8π
Triangles
Triangles deserve an article series of their own; there is a wealth of information the GMAT can expect you to know or figure out about triangles, more than any other figure, because the way triangles work can change according to the type of triangle. The most common aspects tested:
Area (triangle) = ½(base)(height)
Perimeter = a + b + c (where a, b, and c are the sides)
Other things to make sure you know about the triangles you face:
1. What type of triangle is it? An equilateral triangle has three equal sides and three 60° angles, while an isosceles triangle has two equal sides and equal angles opposite those sides; either one may be key to figuring out a question.
2. Is it a right triangle? If one angle of the triangles is 90° then it is a right triangle, and has a separate set of rules that would be shortcuts if the GMAT didn’t expect you to know them. You can use the Pythagorean Theorem (a² + b² = c²) to figure out side lengths, and even use “Pythagorean triplets” to save yourself some math: some right triangles have sides in the common ratios 3:4:5 and 5:12:13 (and their multiples).
3. Do I have multiple similar triangles? Clues that your triangles are similar are three identical angle measures, three proportional sides, or two proportional sides on either side of an identical angle; similar triangles have the same angles and proportional sides. Triangles that are congruent are identical.
Triangle Practice Question
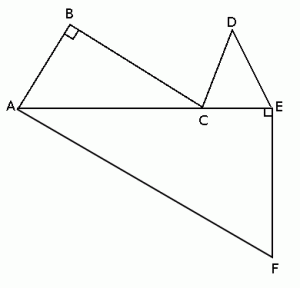
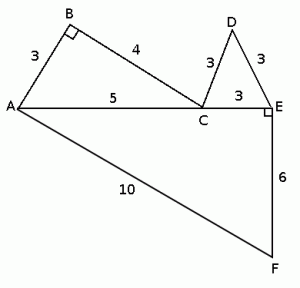
In the figure above, triangle CDE is an equilateral triangle with side length 3, AF = 10, EF = 6, and AB = DE. What is the perimeter of the figure?
(A) 45
(B) 36
(C) 29
(D) 24
(E) 16
Answer and Explanation
The answer is (C) 29. How?
The question tells us this much:
From here, we can deduce that:
1. Triangle AEF is a 3:4:5 triangle, with side lengths 6:8:10, respectively.
2. Since AE is 8 and CE is 3, that makes AC = 5.
3. Since AC = 5, triangle ABC is also a 3:4:5 triangle, and BC = 4
We can then have:
10+6+4+(3*3) = 29. Answer choice (A) 45 is the sum of the perimeters of each of the triangles, rather than the perimeter of the figure.
Mixed Figures
Mixed figures are “simply” combinations of familiar shapes into a single more complex figure. You need to take more care than usual in carrying over information from one type of figure to another; the height of the triangle may be the side of a hexagon inscribed within a circle within yet another triangle, each figure with its own set of formulas for area and perimeter. On the other hand, because a statistically significant number of people have to get the question right for the GMAT to be any good to admissions offices, that same complexity of the figure can lead to simpler calculations. As always, start with what you know, and go from there!
Mixed Figure Practice Question
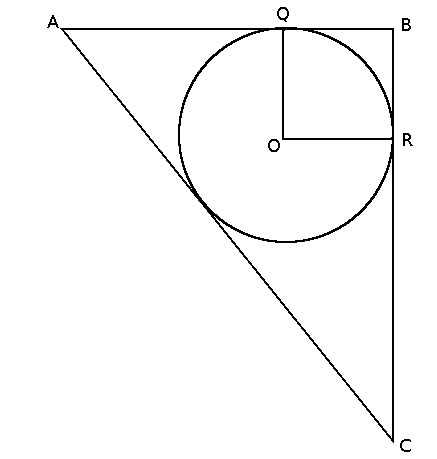
Note: figure not drawn to scale
The playing area for a certain outdoor game requires markings according to the figure shown. The ratio of AB:BC:AC is 3:4:5 ; O is the midpoint of the circle, R and Q are both points on the circle with center O and corners of square OBQR. If QB is 1/3 of AB and a person running in a straight line from Q to R travels 3√2 meters, approximately how many meters of paint are required to paint the playing area on a surface (assume the lines have negligible width)?
(A) 54π
(B) 97
(C) 72
(D) 67
(E) 45
Answer and Explanation
Answer: (D) 67. How?
We know that the ratio of the lengths of the sides x of a square to its diagonal are the same as that of a 45:45:90 triangle: x:x:x√2. You could also use the Pythagorean Theorem, setting 3√2 as the hypotenuse, so (3√2)² = 2*(side length)², so 2s²=18, and s²=9, so the sides are 3 meters each. This is also the radius of the circle, so from here we can figure out:
Perimeter of circle: the circle’s radius is 3, and the perimeter (circumference) is 2πr, or 6π.
Perimeter of square: the square’s perimeter is 4s, or 12.
Perimeter of triangle: since QB is 1/3 of AB and QB = 3, AB = 9. Triangle ABC is in the 3:4:5 ratio, so the other sides are 12 and 15, respectively. 9 + 12 + 15 = 36.
Circle + square + triangle = 6π + 12 + 36 = 48 + 6π, or approximately 48+19 = 67 meters.