ACT Math: Three Dimensional Geometry

Sometimes, there will be questions on the ACT Math section about the volume and surface area of an object. Even though the formulas for some of these shapes will be in the test directions, it is best to memorize them to save time on the test.
We will talk about two basic shapes. The cube and the rectangular solid. In each case, we will talk about finding the volume, the surface area, and the diagonal of each shape.
 

Cubes will be the simplest of all three dimensional geometry, mainly because there is a set formula to find every single value the ACT looks for.
First off, volume is found by multiplying the length x width x height of a solid. But because a cube has all sides equal, the formula is V = s³, where s = the length of the side.
In order to find the surface area, we simply find the area of one of the faces and multiply it by 6. Our formula being SA = 6s², where s = length of the side.
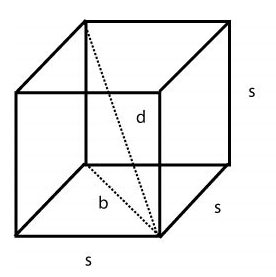
To find the diagonal, is a little tricky. Looking at the diagram below, you see that the diagonal (d) connects two opposite corners of the cube. We can also see that the diagonal of one of the faces (b) and the height of the cube act as two legs of a right triangle, with the diagonal acting as the hypotenuse. This can give us the steps to use in order to find the diagonal of a cube or rectangular solid. We can find the diagonal by using the Pythagorean Theorem.

It is important to know how to find the diagonal manually, especially with rectangular solids, but with cubes, because all sides are equal we can also memorize a formula.
Diagonal for a cube (and ONLY a cube) is d = s√3
 

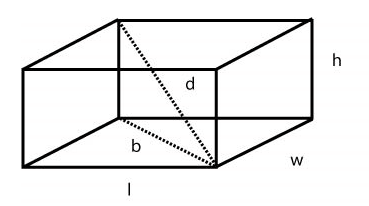
Very similar to cubes, except most likely on the test, they will not have any equal sides. Luckily, the concepts are exactly the same.
Volume is simply V = lwh, where l = length, w = width, and h = height
Surface area is SA = 2lw + 2hl + 2hw
Diagonal is also pretty similar to the cube, in that we use the Pythagorean Theorem to find the diagonal of the solid. Looking at the diagram below, we see that the diagonal (d) is simply the hypotenuse, where as the legs of the triangle are the height (h) and the diagonal of the base (b).