ACT Math: All About Circles

There are four main things you need to know about circles to tackle any ACT Math question.
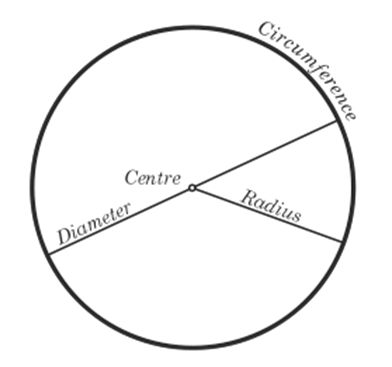
1. The definition of Diameter and Radius. For a pictorial illustration, see the diagram below.
2. The formula for Circumference given by (diameter)(p)
3. The formula for Area given by (p)(radius2)
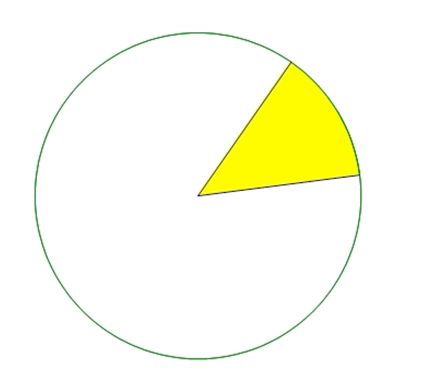
4. Knowing what fraction of the circle the sector is. Note that a sector is what the ‘slice’ in the circle, an example sector is the yellow wedge show in the green circle. The white part of the circle is also known as a sector, even though it doesn’t look like your typical ‘slice’.

Let’s try and apply the concepts to see if you understand.
 

Suppose the diameter of a circle is 12 cm. What would be its circumference? And what would be its area? Simply apply the formulas to get:
circumference – (diameter)(π)-(12)(π)-12π
area-(π)(radius)²-(π)(6)²-36π
Don’t forget that radius is half of the diameter, so if the diameter is 12 cm, the radius is 6 cm.
The question might add another step by telling you that there is another circle with diameter 6 cm and ask how many times bigger, in terms of area, is the circle with diameter 12 cm than this circle? Just because one has diameter 12 cm and the other has diameter 6 cm does not mean that the bigger circle is twice as big.
Use the formulas to figure out that the area of the new circle is 9π cm² while the area of the big circle is 36π cm², as we found out earlier. This means that the bigger circle is 4 times as large as the smaller circle.

The last concept involves applying your knowledge of circumference and area to sectors. Sectors are basically a fraction of the entire circle. If the yellow sector in the circle above had an arc of 45° that means that it is 1/9 of the entire circle, because a circle has 360°. The implications of this are two fold:
1. The arc length of the yellow wedge is also 1/9th of the circumference
2. The area of the yellow wedge is also 1/9th of the area of the circle
Thus, if the radius of that circle was 10 cm, then its circumference would be 10π cm and its area would be 25π cm². Correspondingly, the arc length of the sector would be 10π/9 cm and the area of the sector would be 25π/9 cm².
If the question wants you to find the perimeter of the yellow wedge, all you have to do is add the radius twice to the arc length you found to get (10 + 10π) cm.
Remember these four concepts in mind and you’ll have the tools to solve any circle problem!
 

For practice, you could try solving these practice problems.
1. A circle has area 50π cm2. A second circle has half the area of the first circle. What is the diameter of the second circle?
2. A circle has a shaded sector. The sector is 1/6 of the whole circle. What is the area of the circle if the sector has area 6π cm2 ? What is the diameter of the circle?