GRE Quantitative: Prime Factorization

As any Kaplan GRE Expert will tell you, the Quantitative section is a test of concepts, not calculations. It’s also a psychological test, designed to intimidate the rookie test-taker with big, scary-looking numbers.
Fortunately, there’s always a method to the GRE’s math madness and, consequently, a way of making those intimidating numbers easier to understand. That’s where the factor tree comes in—one of the most powerful weapons to add to your GRE math arsenal.

Factor tree basics

You may remember (fondly or not) making a factor tree in grammar school. Factor trees allow you to break a large number down into smaller, more manageable parts.
First, we should review the basics of how to find prime factors. We begin by using a garden variety factor tree whose fruit is composed of the essence of any positive, non-prime integer.
Suppose we want to find the prime factors of 60:

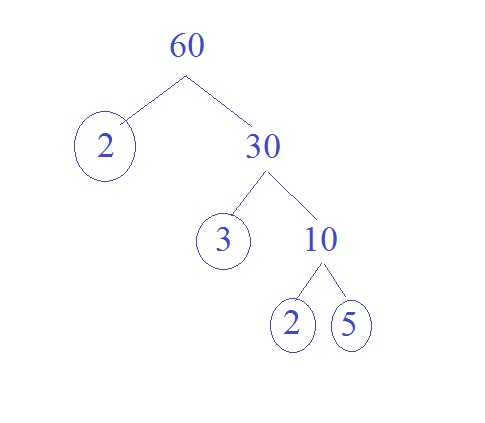
We can start with any two factors of 60 that are each less than 60, but together multiply to 60. Here, we use 2 and 30. Every time you hit a prime number, circle it, because that “branch” of the factor tree has reached its end. In this example, 2 is prime, so we circle it.
Then, we can break down 30 in the same way: We use 3 and 10, circling 3, since it’s prime. We then break 10 into 2 and 5, each of which is prime and gets circled as well.
This tells us a few things about the number 60. First, it tells us that its prime factors are 2, 3, and 5. Perhaps more importantly, it tells us that 60 can be expressed by multiplying all those numbers we circled a moment ago: 2 x 2 x 3 x 5.

Know your prime numbers

A prime number is an integer greater than 1 with exactly two positive factors: 1 and itself. Every integer greater than 1 can be expressed as a product of prime numbers. The number 1 is neither prime nor composite.
It would certainly behoove any aspiring GRE champion to therefore memorize at least the first handful of prime numbers: 2, 3, 5, 7, 11, 13. You’ll notice that 2 is the smallest and the only even prime number. Remember, not all odd numbers after 2 are prime (you’ll notice that 9 is not prime because it is divisible by 3, for instance)—but after 2, all prime numbers are odd.

When to Use Prime Factorization on the GRE

Prime factorization can help solve GRE Quantitative Reasoning problems involving factors, multiples, and divisibility. Common clues include these terms:

• Factor
• Multiple
• Divisible by
• Divides evenly into
• Remainder
• Greatest common factor
• Least common multiple

When a problem includes this language, breaking the numbers into prime factors can reveal relationships that are difficult to see in their original form. This approach can be especially helpful when a question includes large numbers, variables, or exponents.

Making GRE math manageable

Finding prime factors can save you time and effort on the Quantitative section of the GRE if you know how to apply the concept. Whenever you feel like the GRE is trying to make you multiply or divide very large numbers—let’s use the very technical term “BUNs,” or Big Ugly Numbers—there’s a good chance that the shortcut involves prime factorization.
Imagine that the GRE gives you the following equation and asks you to solve for the value of b:

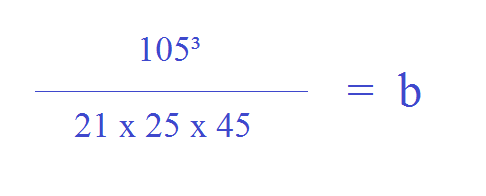
It would be time-consuming and inefficient on Test Day to determine what 105 x 105 x 105 is equal to, then find the actual value of 21 x 25 x 45, and then divide one BUN by another BUN.
The Kaplan-trained student thinks: “The GRE could’ve given me any numbers in the world, so there has to be some reason that they chose these.” In fact, this problem lends itself quite nicely to prime factorization, in which the math itself is relatively innocuous.

Prime factors are your friend

To solve the problem above, let’s start with the denominator. Using factor trees, we find out 21 = 3 x 7, 25 = 5 x 5, and 45 = 3 x 3 x 5.
Now let’s move to the numerator. The problem says 105³—so let’s just start with 105. Just by looking at 105, we know it’s divisible by 5, but 105 is 5 times what? Well, 5 x 20 would equal 100, in which case we’d need one more 5. So, 105 = 5 x 21, and 21 breaks down into 3 x 7 as we saw a moment ago. Therefore, 105 = 3 x 5 x 7. We have 105³, however. So, we must rewrite 3 x 5 x 7 a total of 3 times for the numerator. Now we have:

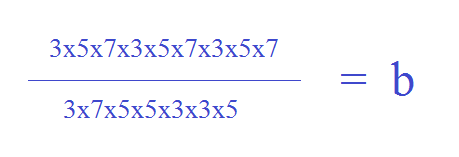
This becomes an exercise in what mathematicians call—to use even more technical terminology—”crossing stuff out.” Let’s cross off as many numbers on the top and bottom as we can, and see what is left standing. Cross out all of the 3’s, all of the 5’s, and just one 7 from the top and bottom—and voila: we are left simply with 7 x 7, or 49.
It involved some writing, but the math itself didn’t hurt too much now, did it?

Using Prime Factorization to Check Divisibility

A positive integer is divisible by another positive integer when its prime factorization contains every prime factor of the divisor, with at least the same exponent.

For example, is 432 divisible by 24?

432 = 2⁴ × 3³
24 = 2³ × 3

The prime factorization of 432 contains enough factors of both 2 and 3 to divide evenly by 24. Canceling the common factors confirms the result:

432 ÷ 24 = 2⁴⁻³ × 3³⁻¹ = 2 × 3² = 18

The same reasoning applies when both expressions contain a common variable factor. For any positive integer n:

432n ÷ 24n = 432 ÷ 24 = 18

The restriction matters: n cannot equal zero because division by zero is undefined.

Finding the Least Common Multiple with Prime Factors

The least common multiple, or LCM, is the smallest positive integer divisible by each of the given numbers. To find it using prime factorization, include each prime that appears in either number, using its highest exponent.

For example, consider 81 and 432:

81 = 3⁴
432 = 2⁴ × 3³

The LCM needs four factors of 2 to cover 432 and four factors of 3 to cover 81:

LCM = 2⁴ × 3⁴ = 16 × 81 = 1,296

Multiplying 81 by 432 also produces a common multiple, but it counts shared prime factors more times than necessary. Using the highest exponent of each prime gives the smallest number divisible by both.

GRE Prime Factorization Practice Question

What is the greatest integer value of n such that 2ⁿ is a factor of 200⁶?

Start by finding the prime factorization of 200:

200 = 2³ × 5²

Next, raise that factorization to the sixth power. When raising a power to another power, multiply the exponents:

200⁶ = (2³ × 5²)⁶ = 2¹⁸ × 5¹²

The prime factorization contains eighteen factors of 2. Therefore, 2¹⁸ divides evenly into 200⁶, but 2¹⁹ does not.

Answer: 18

For problems involving large powers, factoring the base and applying exponent rules can eliminate the need to calculate the full number.

Want to try out your factor tree skills? Sign up for a free GRE practice test and start building the confidence you need to boost your Quantitative score.