PSAT Math: Polynomials

By now you’re used to seeing equations, exponents, and variables; another important topic you are sure to see on the PSAT is polynomials. A polynomial is an expression comprised of variables, exponents, and coefficients, and the only operations involved are addition, subtraction, multiplication, division (by constants only), and non-negative integer exponents. A polynomial can have one or multiple terms.

Note

Remember that a constant, such as 47, is considered a polynomial; this is the same as 47x⁰. Also, keep in mind that for an expression to be a polynomial, division by a constant is allowed, but division by a variable is not.

Identifying like terms is an important skill that will serve you well on Test Day. To simplify polynomial expressions, you combine like terms just as you did with linear expressions and equations (x terms with x terms, constants with constants). To have like terms, the types of variables present and their exponents must match. For example, 2xy and −4xy are like terms; x and y are present in both, and their corresponding exponents are identical. However, 2x²y and 3xy are not like terms because the exponents on x do not match. A few more examples follow:

Like terms	7x, 3x, 5x	3, 15, 900	xy2, 7xy2, –2xy2
Not like terms	3, x, x 2	4x, 4y, 4z	xy 2, x 2y, 2xy

You can also evaluate a polynomial expression (just like any other expression) for given values in its domain. For example, suppose you’re given the polynomial expression x³ + 5x² + 1. At x = –1, the value of the expression is (–1)³ + 5(–1)² + 1, which simplifies to –1 + 5 + 1 = 5.

A polynomial can be named based on its degree. For a single-variable polynomial, the degree is the highest power on the variable. For example, the degree of 3x⁴ – 2x³ + x² – 5x + 2 is 4 because the highest power of x is 4. For a multi-variable polynomial, the degree is the highest sum of the exponents on any one term. For example, the degree of 3x²y² – 5x²y + x³ is 4 because the sum of the exponents in the term 3x²y² equals 4.

On Test Day you might be asked about the nature of the zeros or roots of a polynomial. Simply put, zeros are the x-intercepts of a polynomial’s graph, which can be found by setting each factor of the polynomial equal to 0.

For example, in the polynomial equation y = (x + 6)(x – 2)², you would have three equations: x + 6 = 0, x – 2 = 0, and x – 2 = 0 (because x – 2 is squared, that binomial appears twice in the equation). Solving for x in each yields –6, 2, and 2; we say that the equation has two zeros: –6 and 2.

Zeros can have varying levels of multiplicity, which is the number of times that a factor appears in the polynomial equation. In the preceding example, x + 6 appears once in the equation, so its corresponding zero (–6) is called a simple zero. Because x – 2 appears twice in the equation, its corresponding zero (2) is called a double zero.

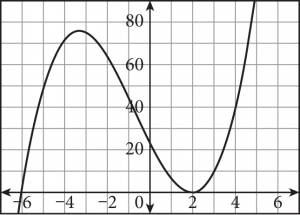
You can recognize the multiplicity of a zero from the polynomial’s graph as well. Following is the graph of y = (x + 6)(x – 2)².

When a polynomial has a simple zero (multiplicity 1) or any zero with an odd multiplicity, its graph will cross the x-axis (as it does at x = –6 in the graph above). When a polynomial has a double zero (multiplicity 2) or any zero with an even multiplicity, it just touches the x-axis (as it does at x = 2 in the graph above).

Use the Kaplan Method for Math to solve this question, working through it step-by-step. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.

Strategic Thinking	Math Scratchwork
Step 1: Read the question, identifying and organizing important information as you go Don’t let the unusual wording fool you. To find how much greater A is, just do what you would do for two numbers: Subtract the smaller from the larger.	A – B
Step 2: Choose the best strategy to answer the question What’s your first step? Substitute the correct expressions for A and B. Distribute the –1 outside the second set of parentheses. Be careful here; this is an easy place to make a mistake. And afterward? Combine like terms. Rearranging so that like terms are next to each other helps here.	(24xy + 13) – (8xy + 1) = 24xy + 13 – 8xy – 1= 24xy – 8xy + 13 – 1= 16xy + 12
Step 3: Check that you answered the right question No further simplification is possible; the correct answer is (C), so you’re done.