PSAT Math: Ratios and Proportions
Ratios and proportions are quite common in everyday life. Whether it’s making a double batch of meatballs or calculating the odds of winning the lottery, you’ll find that ratios and proportions are invaluable in myriad situations.
PSAT Math: Ratios
A ratio is a comparison of one quantity to another. When writing ratios, you can compare part of a group to another part of that group, or you can compare a part of the group to the whole group. Suppose you have a bowl of apples and oranges. You can write ratios that compare apples to oranges (part to part), apples to total fruit (part to whole), and oranges to total fruit (part to whole).
You can also combine ratios. If you have two ratios, a:b and b:c, you can derive a:c by finding a common multiple of the b terms. Take a look at the following table to see this in action.
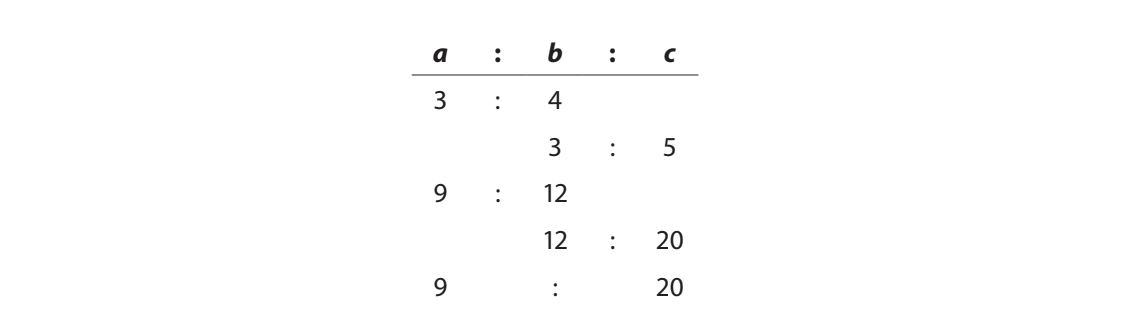
What’s a common multiple of the b terms? The number 12 is a good choice because it’s the least common multiple of 3 and 4 which will reduce the need to simplify later. Where do you go from there? Multiply each ratio by the factor (use 3 for a:b and 4 for b:c) that will get you to b = 12.
The ratio a:c equals 9:20. Notice we didn’t merely say a:c is 3:5; this would be incorrect on Test Day (and likely a wrong-answer trap!).
PSAT Math: Proportions
A proportion is simply two ratios set equal to each other. Proportions are an efficient way to solve certain problems, but you must exercise caution when setting them up. Watching the units of each piece of the proportion will help you with this. Sometimes the PSAT will ask you to determine whether certain proportions are equivalent—check this by cross-multiplying. You’ll get results that are much easier to compare.
Each derived ratio shown except the last one is simply a manipulation of the first, so all except the last are correct. You can verify this via cross-multiplication (ad = bc).
Alternatively, pick numerical values for a, b, c, and d; then simplify and confirm the two sides of the equation are equal. For example, take the two equivalent fractions 2/3 and 6/9 (a = 2, b = 3, c = 6, d = 9).
Cross-multiplication gives 2 × 9 = 3 × 6, which is a true statement. Dividing a and b by c and d gives 2/6 = 3/9 , also true, and so on. However, attempting to equate (a/d)(2/9) and (b/c)(3/6) will not work.
Let’s take a look at a test-like question that involves ratios:
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
| Strategic Thinking | Math Scratchwork |
| Step 1: Read the question, identifying and organizing important information as you go
You need the ratio of methanol to dioxane. You’re given two ratios: dioxane to water and water to methanol. |
D:W = 7:3 W:M = 5:2 |
| Step 2: Choose the best strategy to answer the question How can you directly compare methanol to dioxane? What’s a common multiple of the two water components? The two given ratios both contain water, but the water components are not identical. However, they share a common multiple: 15. Multiply each ratio by the factor that will make the water part equal 15. Merging the two ratios lets you compare dioxane to methanol directly. |
D:W = 7:3 W:M = 5:2
common multiple: 5 x 3 = 15 (7:3) x 5 = 35:15 |
| Step 3: Check that you answered the right question
The question asks for methanol to dioxane, so flip your ratio, and you’re done. Choice (D) is correct. Watch out for trap answer A. You aren’t looking for dioxane to methanol. |
M:D = 6:35 |
Note
Beware of trap answers that contain incorrect ratios. Always confirm that you’ve found the ratio requested.
