PSAT Math Quiz: Systems of Equations
Try our Systems of Equations quiz featuring free practice questions for the math section of the PSAT below.
Content Review:
- PSAT Math: Systems of Equations
- PSAT Math: Combination/Substitution
- PSAT Math: Word Problems and Multiple Equations
Test your PSAT readiness by taking this PSAT Math quiz!
Answer 1
C: Create a system of two linear equations where t represents tables with 2 chairs and f represents tables with 4 chairs. The first equation should represent the total number of tables, each with 2 or 4 chairs, or t + f = 25.
The second equation should represent the total number of chairs. Because t represents tables with 2 chairs and f represents tables with 4 chairs, the second equation should be 2t + 4f = 86.
Now solve the system using substitution. Solve the first equation for either variable, and substitute the result into the second equation:
t + f = 25 –> 25 – f
2 (25 – f) + 4f = 86
50 – 2f + 4f = 86
2f = 36
f = 18
There are 18 tables with 4 chairs each, (C). This is all the question asks for, so you don’t need to find the value of t.
PSAT Math Systems of Equations Question 2
If (x, y) is the solution to the system of equations graphed in the figure, what is the value of x + y ?
A. -2
B. -1
C. 1
D. 4
Answer 2
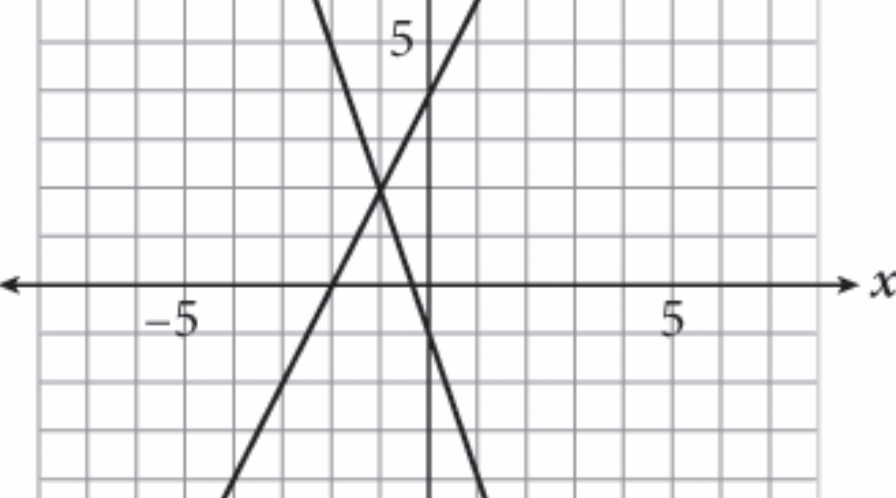
C: Graphically, the solution to a system of linear equations is the point where the lines intersect. Jot down the coordinates of the point on the graph where the two lines intersect, (01, 2). The question asks for the sum of x + y, so add the coordinates to get =1 + 2 = 1. Choice (C) is correct.
Answer 3
C: Translate English into math to write a system of equations with t being the cost of a turkey burger and w equaling the cost of a bottle of water. The first statement is translated as 2t + w = $3.25 and the second as 3t + w = $4.50.
The system is:
2t + w = 3.25
3t + w = 4.50
You could solve the system using substitution, but combination is quicker in this question because subtracting the first equation from the second eliminates w and you can solve for t:
3t + w = 4.50
– (2t + w = 3.25)
t = 1.25
Substitute this value for t in the first equation and solve for w:
2(1.25) + w = 3.25
2.5 + w = 3.25
w = 0.75
Two bottles of water would cost 2 x $0.75 = $1.50, which is (C).
Previous: PSAT Math Quiz: Equations and Word Problems
Next: PSAT Math Quiz: Rates, Ratios, Proportions, and Percents
